Combat de Poule
Prenons un sport, le Judo par exemple. Dans les compétitions de Judo il y a des groupements de compétiteurs, appellés “poules” (les groupements, pas les compétiteurs). Chacun doit combattre contre tous les autres adversaires de la poule, afin d’établir un classement, dont le premier, et parfois le deuxième peuvent continuer la compétion : huitème de finale, quart, demi et finale.
Question : Combien de combats sont organisés par poule?
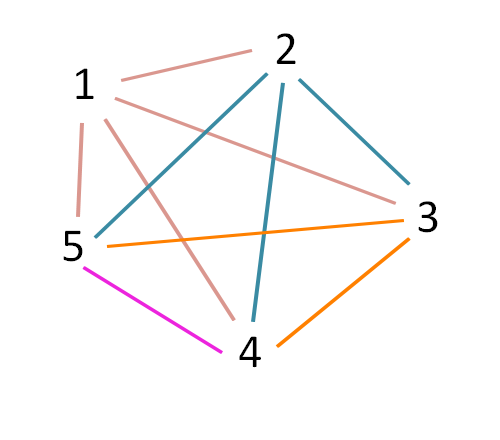
On va modéliser le problème avec un graphe : les noeuds représentent les combattants, les arcs les combats entre judokas. Une bonne méthode pour comprendre est de reconstruire l’ensemble des combats qui auront lieu.
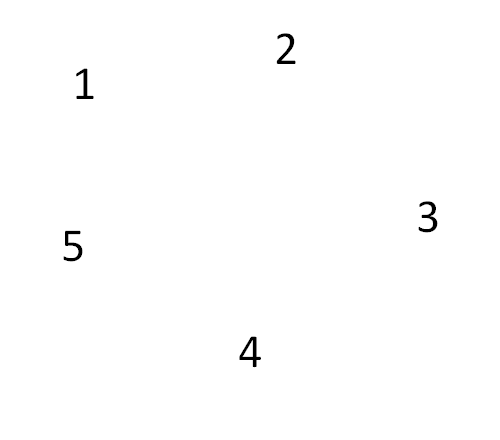
Chaque numéro correspond à un combattant
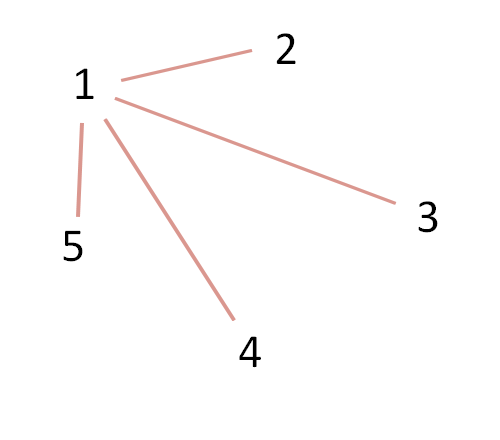
Pour n combattants, le combattant 1 aura n-1 rencontres, car il rencontre chacun des autres adversaires (il ne combat pas contre lui-même bien évidemment), on tisse donc n-1 arcs.
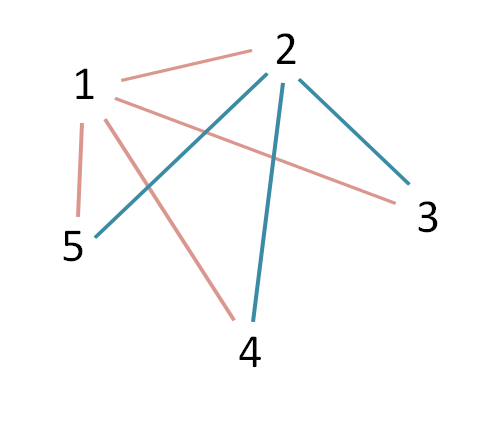
Le combattant 2 aura n-1 randoris aussi, mais l’arc vers le combattant 1 a déjà été tissé, on ne tisse donc que n-2 liens.
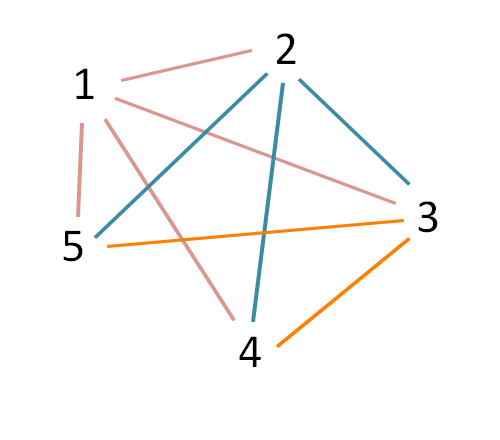
Et ainsi de suite
Le nombre total de liens tissés est donc :
\[(n-1) + (n-2) + (n-3) + ... + 1 + 0 = \sum_{k=1}^{n-1}n-k = \sum_{k=1}^{n-1}k = \frac{n(n-1)}{2}\]Car il s’agit d’une suite arithmétique de raison 1 commençant à 1.
Soit dit en passant, ce problème est celui du nombre d’arcs dans un graphe complet.
Ce qui signifie que pour une poule de 5, on a 10 rencontres, pour une poule de 6 on a 15 rencontres. Au delà, on commence à avoir trop de rencontres (Imaginez des poules de 10, on aurait 45 rencontres), ce qui fait trop durer la compétition, c’est pourquoi on voit rarement des poules contenant plus de 6 personnes.