Combien de zones dans ce cercle ?
Position du problème
On dispose d’un cercle dans lequel un nombre n de points ont été disposés le long de son périmètre. Les points sont ensuite reliés deux à deux, comme sur la figure ci-contre, ce qui génère une figure géométrique.
Combien existe-t-il de zones ?
Ce premier problème provient d’une correpondance de Dijsktra : https://www.cs.utexas.edu/users/EWD/ewd10xx/EWD1017.PDF
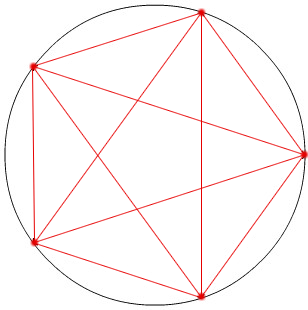
Notons qu’ici j’ai représenté les points à intervalles réguliers sur le périmètre du cercle de sorte à obtenir une belle figure géométrique régulière, mais on pourrait tout aussi bien les placer n’importe où sur le périmètre (du moment qu’ils ne se confondent pas), cela ne changerait pas le problème. Résolution du problème
Posons n = nombres de points et f = nombre de zones.
Une restriction cependant : deux points d’intersection entre des lignes ne peuvent pas être confondus. Autrement dit, on a au maximum deux lignes qui se coupent en un même point. On ne peut donc pas avoir la disposition suivante (pour n =6):
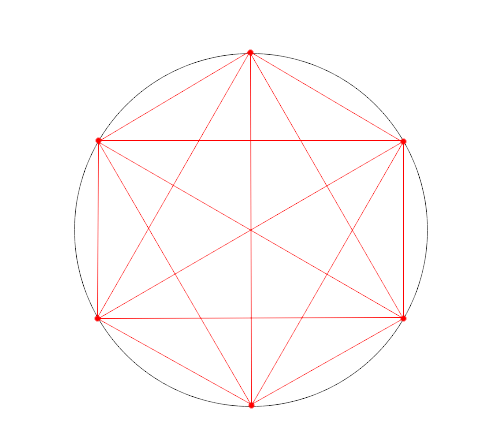
Figure impossible d’après nos restrictions
Mais plûtôt quelque chose du style:
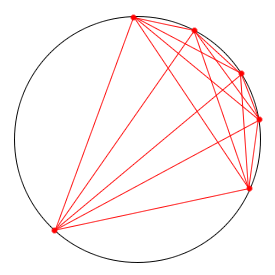
Mais celle-là oui !
En tracant les différents cas, on pourrait se dire que la formule qui décrit le nombre de parties est f = 2n-1. Mais si on regarde pour n = 6, on a 26-1 = 32, et on trouve 31. Cette formule ne fonctionne donc pas pour ce problème.
Pour touver la solution, trouvons plusieurs indices qui vont nous guider dans notre raisonnement.
Nous allons raisonner en imaginant que nous construisons la figure, en ajoutant les cordes une à une (j’utiliserai parfois le terme corde à la place de ligne).
Indice 1 : L’ajout d’une corde sur la figure ajoute un nombre de parts coupés à la figure
Indice 2 : Ce nombre de nouvelles zones est égale au nombre de segments sur la nouvelle corde
Indice 3 : Le nombre de segments sur une nouvelle corde est lui-même égale au nombre d’intersections sur cette corde, plus 1. 2 zones à l’origine. On ajoute une corde, ce qui fait ici 2 segments, càd 1 intersection, càd 2 nouvelles zones.
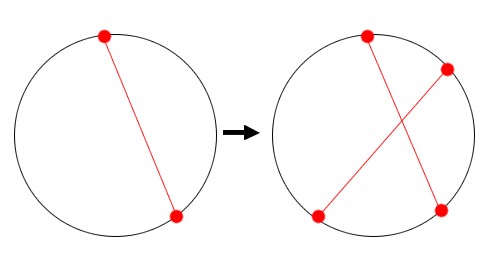
Ainsi, on trouve que l’ajout d’une corde à la figure entraine la création de :
\[\Delta f = 1+nbIntersectionsCorde\]zones.
Si on répète ce processus autant de fois qu’il y a de cordes, on trouve :
\[f=nbCordes+nbIntersections+1\]En effet, à chaque ajout d’une nouvelle corde, les nouvelles intersections créées sont comptabilisées, et puisqu’une intersection correspond à la rencontre d’exactement deux cordes (et pas plus !), ce processus itératif va bien prendre en compte chacune des intersections une seule fois. Le + 1 à la fin correspond au fait qu’initialement le cercle vide contient une seule zone.
On peut maintenant trouver f en fonction de n : le nombre de cordes correspond au nombre de façons de sélectionner 2 points parmis n (puisqu’on relie toutes les cordes possibles), et le nombre d’intersections correspond au nombre de façons de sélectionner 4 points parmis n. Pourquoi 4? Parce qu’il faut deux cordes pour faire une intersection, donc 4 points.
On a alors :
\(f=\binom{n}{2}+\binom{n}{4}+1\)
\(f = \frac{n}{(n-2)!2!} + \frac{n}{(n-4)!4!} + 1\)
\(f = \frac{n*(n-1))}{2} + \frac{n*(n-1)*(n-2)*(n-3)}{24} + 1\)
\(f = \frac{n^4-6n^3+23n^2-18n}{24} + 1\)
\(f = \frac{n^4}{24} - \frac{n^3}{4} + \frac{23n^2}{24} + \frac{3n}{4} + 1\)
En utilisant la propriété des coefficients binomiaux suivante:
\[\binom{n}{k} = \binom{n-1}{k-1}\binom{n-1}{k}\]on peut mettre cela sous la forme :
\[\binom{n}{k} = \binom{n-1}{0} + \binom{n-1}{1} +\binom{n-1}{2} +\binom{n-1}{3} +\binom{n-1}{4}\]Ce qui correspond à la somme des 5 premiers éléments d’une ligne du triangle de Pascal, comme nous le fait remarquer Dijsktra. Notons que la somme des éléments d’une ligne du triangle de Pascal vaut 2numeroLigne. Donc pour n < 6, on ne voit pas la différence avec la conjecture qu’on a faite au début, à savoir dire qu’il y a 2n zones. Mais dès qu’on arrive à l’étape 6, et bien on ne prend que les 5 premiers éléments de la ligne, donc on vire le dernier 1, ce qui donne 31 au lieu de 32 !
NB: Notons que 2 parmis n donne n(n-1)/2, ce qui correspond bien au nombre de liens d’un graphe complet, autrement dit au nombre de rencontres dans une “poule” de taille n.
Autre problème :
Un autre problème, plus simple, m’a été proposé par un ami. On a un cercle, dans lequel on effectue n sections rectilignes, qui traversent tout le cercle. Combien de zones obtient-on au maximum?
NB: Pour le min c’est simple, il suffit de tracer toutes les sections de manière paralléles, et on trouve n+1 zones.
Pour trouver le max, on réflechit de la même manière que pour le problème précédent, à savoir par construction. Au début on ajoute une section, ce qui nous donne deux zones. Lorsqu’on ajoute une deuxième, on a 4 zones. Pour la troisième, si on cherche à faire le maximum de zones, on se rend vite compte qu’il faut que cette section traverse les deux précedentes, ce qui nous donne 7 zones. etc.
Indice : Au rang n, pour maximiser le nombre de zones, il suffit de tracer une nouvelle section qui traverse les n-1 autres sections.
Ainsi, à chaque étape de construction, le nombre de zone est égale au nombre de zones déjà existantes, plus le nombre de sections déjà existantes, plus 1:
\[fn = n-1+f_{n-1}+1=n+f_{n-1}=n+(n-1)+f_{n-2}=\frac{n(n+1)}{2}\]On trouve donc la suite arithmétique de raison 1 commençant par 1.
J’en profite pour placer une démonstration particulièrement élégante du nombre de termes de cette suite. Je crois que c’est Gauss qui avait trouvé ça quand il était enfant.
\[fn=1+2+...+n−1+n\]Mais on peut aussi l’écrire dans l’autre sens:
\[fn=n+n−1+...+2+1\]Et du coup, si on somme les deux, on trouve :
\[2fn=(n+1)+(n+1)+...+(n+1)+(n+1)\]et donc : \(fn=\frac{n(n+1)}{2}\)