Eight Queens Puzzle
The eight queens puzzle is a classic algorithmic problem.
# Problem You have a chessboard of 8*8 square. You have 8 queens. Your goal is to place the 8 queens on the board, without any of them threatening another one. A queen is threaten if she is on the same row, or the same column, or the same diagonal of another queen (like in the rules of chess).
# Solutions A brute-force approach may take too much time here, because we have 8 among 64 possibilities. The interesting thing about this problem is that you have different approaches to solve it (check on Wikipedia): brute-force, dynamic programming, genetic algorithms…
An interesting (and simple) approach is the ‘iterative repair’. The idea is to place a queen on each row, with a random position on this row. Then, we find the queen the more threaten, and we change her location on the same row : it is the repair operation. Here, I chose a new random position on the row, but selecting the position with the less conflict should be a very efficient heuristic (I kept it simple in a first time).
This way of solving the problem is a greedy one. So, it can stay on a local extremum without finding a global one (= a solution). A solution to that is to give a count that you decrement each time you “repair” the current configuration. If that count is reached without finding that the current configuration is a solution, we consider that we are on a local extremum, we will not find a solution, so we generate another configuration.
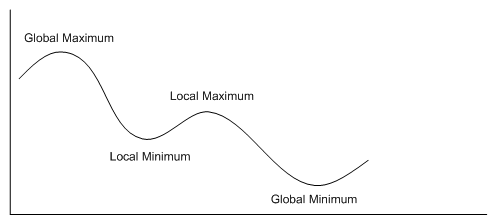This function represents all possible configurations. When we reach a minimum, it is a solution. There are configurations when we stay in the local minimum, repairing after repairing we move a little on the curve but we stay here !
Another thing with this algorithm is that it will find a solution, not necessarily all the solutions (or you must repeat the algorithm but there is clever things to do if you want to find all solutions). But if you want to find a solution quickly, even on a big chessboard, this solution is good. In fact it works on way bigger chessboard : with 1 000 000 queens, the algorithm with the optimization of selecting the best next place when “repairing” takes 50 steps in average.
# coding: utf-8
import time
from random import randint
PROBLEM_SIZE = 8
# the 0 means no queen on this location, 1 that there is one.
game_board = [[0 for i in range(PROBLEM_SIZE)] for j in range(PROBLEM_SIZE)]
def init_board(game_board):
#we place a queen on each row
for i in range(len(game_board)):
game_board[i][randint(0,PROBLEM_SIZE-1)] = 1
def count_conflict(game_board, x, y):
"""give the number of conflict for the position x,y"""
count = 0
# we check the top
for k in range(x-1,0,-1):
if game_board[k][y] == 1:
count += 1
# we break because the current queen will not affect
# other queen behind the one we just found
break
# we check the left
for l in range(y-1,0,-1):
if game_board[x][l] == 1:
count += 1
break
# we check the bottom
for k in range(x+1,len(game_board)):
if game_board[k][y] == 1:
count += 1
break
# we check the right
for l in range(y+1,len(game_board[x])):
if game_board[x][l] == 1:
count += 1
break
#we check the upper left diagonal:
if(x-1 >= 0 and y-1 >= 0):
next_location = (x-1,y-1)
while(next_location[0] >= 0 and next_location[1] >= 0):
if(game_board[next_location[0]][next_location[1]] == 1):
count += 1
break
next_location = (next_location[0]-1, next_location[1]-1)
#we check the bottom left diagonal:
if(x+1 < len(game_board) and y-1 >= 0):
next_location = (x+1,y-1)
while(next_location[0] < len(game_board) and next_location[1] >= 0):
if(game_board[next_location[0]][next_location[1]] == 1):
count += 1
break
next_location = (next_location[0]+1, next_location[1]-1)
#we check the bottom right diagonal:
if(x+1 < len(game_board) and y+1 < len(game_board[x])):
next_location = (x+1,y+1)
while(next_location[0] < len(game_board) and next_location[1] < len(game_board[x])):
if(game_board[next_location[0]][next_location[1]] == 1):
count += 1
break
next_location = (next_location[0]+1, next_location[1]+1)
#we check the upper right diagonal:
if(x-1 >= 0 and y+1 < len(game_board[x])):
next_location = (x-1,y+1)
while(next_location[0] >= 0 and next_location[1] < len(game_board[x])):
if(game_board[next_location[0]][next_location[1]] == 1):
count += 1
break
next_location = (next_location[0]-1, next_location[1]+1)
return count
def check_configuration(game_board):
"""This function test if we are in a good configuration.
If yes, it returns true, if not, it returns the location of the more conflicting queen """
# key is the location of the queen, second is the number of conflict
conflict_count = {}
for i in range(len(game_board)):
for j in range(len(game_board[i])):
if(game_board[i][j] == 1):
# we add this queen if we do not have found her yet
conflict_count[(i,j)] = count_conflict(game_board,i,j)
more_conflicting = max(conflict_count, key=conflict_count.get)
if(conflict_count[(more_conflicting[0], more_conflicting[1])] == 0):
return True
else:
return more_conflicting
def print_game_board(game_board):
for i in range(len(game_board)):
print(game_board[i])
def main(game_board):
init_board(game_board)
more_conflicting = check_configuration(game_board)
# let's say we let our algorithm try 1000 times from an initial configuration. If we can't find
# a solution, we try with another random generation
count = 100
while(more_conflicting != True):
# we change the location of the queen
game_board[more_conflicting[0]][more_conflicting[1]] = 0
game_board[more_conflicting[0]][randint(0,PROBLEM_SIZE-1)] = 1
more_conflicting = check_configuration(game_board)
if count == 0:
init_board(game_board)
count = 100
count -= 1
#print_game_board(game_board)
main(game_board)
If we want to find all solutions, we can make a brute-force algorithm with a little of help : we begin the search from a configuration where there is a queen on each row (\(8^8 = 16,777,216\) possibilities). If we do this with a DFS, row by row, we can eliminate many solutions soon in the search tree (it is the same idea as a branch-and-bound approach, you cut branches that you know are not good solutions).
Now the smarter version of the iterative repair is to choose the square with the less threatening, in the same row. You just need to change a little bit of code at the end :
def main(game_board):
init_board(game_board)
more_conflicting = check_configuration(game_board)
# let's say we let our algorithm try 1000 times from an initial configuration. If we can't find
# a solution, we try with another random generation
count = 100
while(more_conflicting != True):
# we change the location of the queen
game_board[more_conflicting[0]][more_conflicting[1]] = 0
best_position = (-1,-1)
score_best_position = float('inf')
# we find the best place on the same row
for j in range(PROBLEM_SIZE):
buff = count_conflict(game_board, more_conflicting[0], j)
if(buff < score_best_position):
score_best_position = buff
best_position = (more_conflicting[0], j)
game_board[best_position[0]][best_position[1]] = 1
more_conflicting = check_configuration(game_board)
if count == 0:
init_board(game_board)
count = 100
count -= 1
Results
So now, let’s see the difference between solutions : random, stupid iterative repair (random queen on the same row), smarter iterative repair (we place the queen in the square of the row where the threatening is the lowest):
As we can see, with small problems, the “stupid repair” works even better than a smarter approach. On bigger problems though, we see the huge difference between them.