Faux positifs
En statistique et en machine learning, on utilise souvent la notion de “faux positifs”, “vrai positifs”, rappel, précision … Nous allons expliquer ces concepts aujourd’hui.
Contexte (classifieur binaire)
Admettons qu’on ait une application de machine learning, qui permette de classifier les concombres. Dans un premier temps restons simple, gardons deux classes (classifieur binaire): les concombres et les non-concombres. Pour l’utilisateur, c’est très facile, il donne une photo au classifieur, et celui-ci lui-répond s’il s’agit d’un concombre ou pas. Bien.
Des faux positifs ?
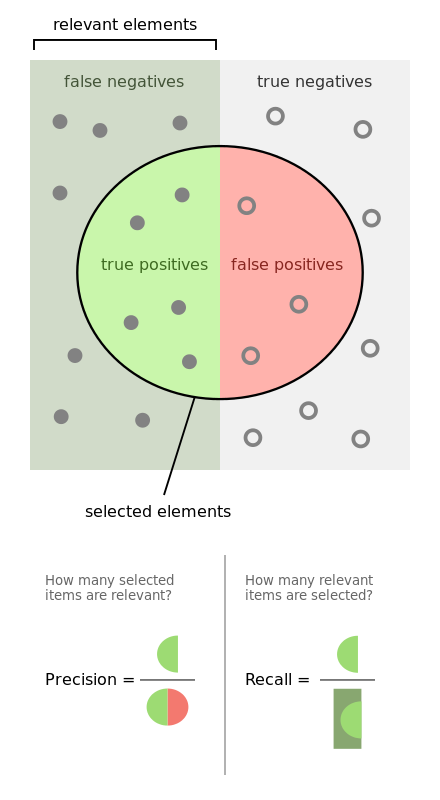
Notre application ne peut pas être parfaite, vous vous en doutez bien. Il y aura forcément des cas où elle détectera une image comme étant un concombre alors que ça n’en est pas un, ou l’inverse. C’est ici qu’interviennent ces notions de faux positifs, vrais négatifs, que voici:
- Faux positifs: les images de “non-concombre” détectées comme “concombres” par notre application (erreur)
- Vrais positifs: les images de “concombre” détectées comme “concombres” (correct)
- Faux négatifs: les images de “concombre” detectées comme “non-concombres” (erreur)
- Vrais négatifs: les images de “non-concombre” détectées comme “non-concombres” (correct)
En vérité, retenir la proposition suivante vous assure de ne plus vous tromper:
L’utilisation du terme “positif” signifie que l’application a détecté l’image comme étant un concombre, et la notion de vrai ou de faux indique si cette détection est juste ou pas.
Mesurer la qualité d’un classifieur
La précision
La formule de la précision est simple :
\[Precision = \frac{VraiPositifs}{VraiPositifs + FauxPositifs}\]C’est le nombre de concombres réels détectés divisé par le nombre total de détections.
La précision indique à quel point le classifieur est juste, càd le pourcentage de chance qu’il ne se trompe pas, pour une classe donnée.
Le rappel
La précision ne suffit pas à évaluer la qualité d’un classifieur, voici pourquoi. Imaginez que nous ayons 7 photos de concombres, et 3 photos de non-concombres. Admettons que notre classifieur détecte 2 concombres qui sont rééllement des concombres, et le reste en non-concombres. En reprenant la formule de la précision, on se retrouve avec 2 vrai positifs et 0 faux positifs, on à alors une précision de 100% pour la classe concombre, càd notre classifieur ne se trompe jamais quand il détecte un concombre. C’est vrai, mais en attendant il en a detecté très peu! C’est là qu’intervient le rappel:
\[Rappel = \frac{VraiPositifs}{VraiPositifs + FauxNégatifs}\]C’est le nombre de concombres détectés qui sont de vrais concombres divisés pas le nombre total de concombre détectables.
Le rappel indique à quel point le classifieur couvre les données, càd le pourcentage d’éléments qu’il détecte par rapport à l’ensemble d’éléments détectables pour une classe donnée
F-mesure
Avoir une seule mesure pour qualifier un classifieur est plus commode, c’est pourquoi on utilise souvent un indicateur appellé la F-mesure, dont voici la formule:
\[Fmesure = 2\times\frac{Precision\times Rappel}{Precision+Rappel}\]Cas général (classifieur multiclasses)
Un classifieur multiclasses est un classifieur qui peut prédire la classe d’un élément parmi plus de deux classes. Dans notre cas ça pourrait être le fait de différencier des images de concombres en catégorisant de 1 à n, 1 étant un concombre de mauvaise qualité, et n un concombre de top qualité. Pour calculer la précision et le rappel, il faut calculer la précision et le rappel pour chacune des classes, et faire la moyenne :
\[PrecisionMoyenne = \sum\frac{iPrecision}{n}\] \[RappelMoyen = \sum\frac{iRappel}{n}\] \[Fmesure = 2\times\frac{PrecisionMoyenne\times RappelMoyen}{Precision+Rappel}\]Remarques
(je ne sais pas si c’est d’un grand interêt mais j’ai trouvé ces quelques trucs, je les mets là on ne sait jamais …)
Dans le cas particulier du classifieur binaire, on peut constater qu’il y a une symétrie entre les deux classes :
- un vrai positif pour une classe est forcément un vrai négatif pour l’autre, et inversement: si le classifieur décrète qu’il s’agit de la première classe, alors cela implique qu’il ne s’agit pas de la deuxième classe (donc “positif” devient “négatif”), et s’il a bien fait de détecter la première classe, alors il aura bien fait de ne pas détecter la deuxième (donc on reste “vrai”).
- un faux négatif pour une classe est forcément un faux positif pour l’autre : même raisonnement que précédemment.
Un petit récapitulatif pour finir :