Intro

J’ai fait un article sobrement nommé introduction à la DP. On m’a très justement fait remarquer que l’exemple du sac à dos est trop compliqué pour bien comprendre la programmation dynamique si on en a jamais fait. Qu’à cela ne tienne, voici l’intro de l’intro à la DP !

Suite de Fibonnaci

Un problème plus simple pour illustrer la programmation dynamique est celui de la suite de Fibonacci.

Leonardo Fibonacci, un BG du croix baton baton baton siècle

La suite de Fibonnaci est définie comme suit:
\(Fibo(0) = 1, Fibo(1) = 0\) \(Fibo(n) = Fibo(n-1) + Fibo(n-2)\)

A la base, elle était faite pour modéliser l’évolution d’une population de lapins, avec les règles suivantes:

  • Un couple de lapins donne naissance à un autre couple de lapins
  • Un couple de lapins qui vient de naître doit attendre un an avant de pouvoir se reproduire.

Combien aura-t-on de lapins au bout de n années ?

Et bien la solution c’est la suite de Fibonacci, et le plus simple pour le comprendre est de regarder le schéma suivant (fait avec amour):

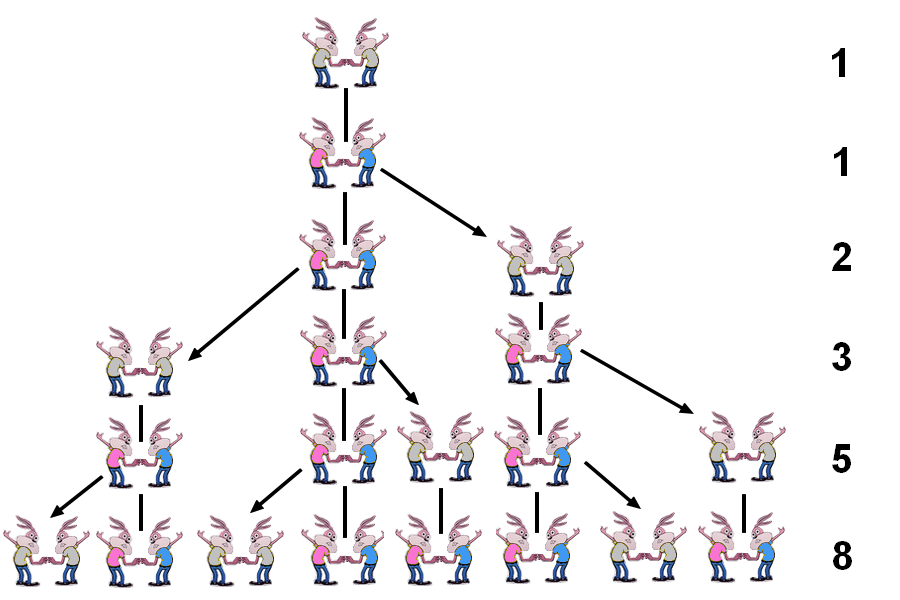Les lapins en gris ne peuvent pas encore se reproduire, les autres oui. Au rang n, on a le nombre de couples de lapins du rang n-1, auquel on ajoute tous les nouveaux nées, ce qui correspond au nombre de couples de lapins du rang n-2. En effet, parmis les lapins du rang n-1, certains ne peuvent pas encore se reproduire, par contre tous ceux du rang n-2 le peuvent.

Elle est où la DP ?

J’y arrive. Si on pose le problème “Combien vaut la suite de Fibonacci au rang n ?”, on pourrait être tenté de faire un algo naif récursif de ce type:

def Fibo(n):
  if n == 0 or n == 1: 
    return 1
  else:
    return Fibo(n-1)+Fibo(n-2)
print(Fibo(10))

89

Le problème avec cette implémentation, c’est qu’on refait plusieurs fois les mêmes calculs ! En effet, si on dessine les appels successifs à Fibo(4), par exemple, on obtient ça:

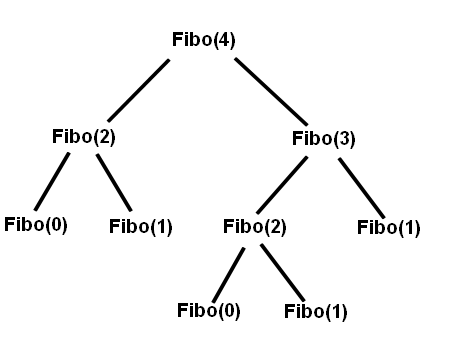
On voit bien qu’on effectue le calcul Fibo(2) deux fois. En fait, si on dessine pour un n plus grand, on voit qu’on a un graphe qui ressemble à un arbre binaire, et qu’on a un algo de complexité O(2^n).

Programmation dynamique Top-Bottom

En gros il y a deux principales méthodes de programmation dynamique. La première, Top-Bottom consiste à stocker les résultats intermédiaires de calcul, en partant du problème au rang n. On part du top (rang n), et pour résoudre ce problème on va résoudre des problèmes plus vers le “bottom” (donc des sous-problèmes, les rangs 0 et 1 correspondant au bottom). On stocke au passage les résultats (mémoïzation), pour qu’à chaque fois qu’on résout un sous-problème on ait pas à le re-résoudre.

n = 10
t = [1,1]+[0 for i in range(2,n+1)]

def Fibo(n):
  if t[n] != 0:
    return t[n]
  else:
    t[n] = Fibo(n-1)+Fibo(n-2)
    return t[n]
    
print(Fibo(10))

89

La complexité de cet algo est de O(n), grâce à la mémoïzation, puisqu’en fait on ne fait le calcul qu’une fois pour chaque rang, de 2 à n.

Programmation dynamique Bottom-up

La deuxième méthode de programmation dynamique est le Bottom-up. L’idée est toujours de garder les résultats intermédiaires, mais cette fois on commence par résoudre le problème au rang le plus bas (2 ici, le bottom), et on “monte” vers des problèmes plus haut (up) en utilisant les résultats qu’on a calculé.

def Fibo(n):
  t = [1,1]+[0 for i in range(2,n+1)]
  
  for i in range(2,n+1):
    t[i] = t[i-1] + t[i-2]
  
  return t[n]
    
print(Fibo(10))

Et là aussi, on est sur une complexité de O(n).

Voilà, vous devriez être parés pour comprendre une dp un peu plus compliquée