Résumé de statistiques bayesiennes
Préambule:
Comme l’article sur les probabilités, il s’agit ici d’un résumé de cours du MIT trouvable ici. L’inférence Bayesienne est nouvelle pour moi, il est possible que certains éléments soient faux. Dans ce cas, et si vous le souhaitez, vous pouvez me laisser un commentaire afin que je corrige l’article.
Loi de Bayes
L’inférence bayésienne se base sur la loi de Bayes:
\[p(A|B) = \frac{p(B|A)p(A)}{p(B)}\]Estimateur du maximum de vraisemblance.
(Maximum Likelihood Estimates, MLE)
C’est une méthode permettant d’estimer la valeur d’un paramètre pour une distribution de probabilités données.
Par exemple si on sait que la durée de vie d’une lampe se modélise bien par une loi exponentielle, et qu’on a 5 ampoules qui ont vécues 2, 3, 1, 3 et 4 ans, on peut faire une estimation du paramètre lambda, grâce au MLE.
| $$f(x1, x2, x3, x4, x5 | \lambda) = (\lambda e^{-\lambda x1})(\lambda e^{-\lambda x2})(\lambda e^{-\lambda x3})(\lambda e^{-\lambda x4})(\lambda e^{-\lambda x5}) = \lambda^{5}e^{-\lambda(x1+x2+x3+x4+x5)}$$ |
| $$f(2, 3, 1, 3, 4 | \lambda) = \lambda^{5}e^{-13\lambda}$$ |
Le but est ensuite de trouver pour quelle valeur de lambda cette probabilité est maximale. Pour cela, on dérive la fonction selon lambda, on trouve pour quelle valeur elle s’annule, on vérifie qu’on est bien sur un max et pas un min. Par soucis de simplification, on préfère dériver le logarithme de la fonction. Ici on a donc:
\(\frac{\partial ln(\lambda^{5}e^{-13\lambda})}{\partial \lambda} = \frac{5}{\lambda} - 13 = 0\) \(\lambda = \frac{5}{13}\)
Exemple
On a une classe de taille n, chaque étudiant possède un numéro unique. On en prend 3 au hasard, et on trouve les nombres 1, 3, 7. Trouver le maximum de vraisemblance. On considère que les numéros sont issus d’une distribution uniforme.
La probabilité de tirer 3 numéros différents est de :
\[\frac{1}{\dbinom{n}{3}} = \frac{3!}{n(n-1)(n-2)}\]car il n’existe qu’une combinaison qui sélectionne ces 3 éléments parmi n.
NB: On peut trouver cette probabilité autrement. On peut se dire que cette expérience revient à prendre un élément parmi n, puis un parmi n-1, puis un parmi n-2. Ceci nous donne une probabilité de :
\[\frac{1}{n(n-1)(n-2)}\]En faisant cela, on a considéré la probabilité de tirer 1, puis 3, puis 7. Mais vu qu’on se moque de l’ordre, il faut aussi rajouter la possibilité de prendre 317, 731 etc, càd le nombre d’arrangement sans remise de k parmi k, soit 3! ici.
| Finalement, il n’est pas vraiment nécessaire d’appliquer complétement la méthode du maximum de vraisemblance, puisque on voit directement que plus n est petit, plus la probabilité p(data | n) est forte, dans la limite où n ne peut pas être plus petit que 7. On a donc un MLE pour n = 7. |
Mise à jour bayésienne
L’idée générale est qu’on va faire une ou des hypothèses, et qu’on va calculer leur probabilités a priori. Ensuite, on va récolter des données. Ces données vont nous donner de l’information pour mieux approximer ces probabilités, cela nous donne la probabilité postérieure.
Par exemple dans le cas d’un détecteur de maladie, avec un taux de vrai positifs de 99%, et un taux de faux positifs de 2%, sachant que la proportion de la population qui est malade est de 0,5%, la probabilité d’être malade si le test est positif est de (NB: H+ c’est être malade, T+ c’est être détecté):
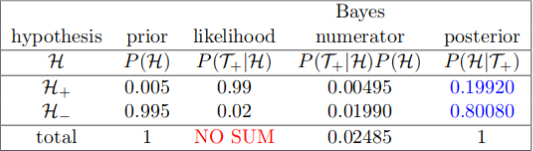
Le principe est qu’on va maintenant pouvoir réutiliseggr le posterior pour faire de nouveaux calculs si on a une nouvelle expérience. Par exemple disons qu’on est dans la situation où le test qui nous a été donné est positif. Disons que quelqu’un qui est atteint de la maladie à 10% de chances de ne pas faire de sport (c’est complètement faux, je dis ça juste pour l’exemple). Notons S- et S+ le fait de faire du sport ou pas. Du coup la probabilité que la personne fasse du sport sachant qu’elle a été testée positive est donc, d’après la loi des probabilités totales:
| $$p(S+ | T+) = p(S+, H+ | T+) + p(S+, H- | T+) $$ | |
| $$= p(S+ | H+)p(H+ | T+) + p(S+ | H-)p(H- | T+)$$ |
On peut aussi utliser la mise à jour bayésienne avec des fonctions continues, que ce soit pour le prior ou bien la probabilité pour la donnée. L’idée est de proposer une approximation du prior (une loi uniforme si on a aucun idée), de récolter les données et d’obtenir une nouvelle approximation (le posterior), grâce à cette donnée. Voir ici.
Conjugate prior
On dit qu’une distribution est un “conjugate prior” pour une autre distribution si la posterior est du même type que la première. Par exemple la distribution beta est le “conjugate prior” de la distribution binomiale. C’est assez pratique, cela signifie qu’il faut juste mettre à jour un paramètre plutôt que de devoir recalculer entièrement une intégrale. A noter que les formules pour les fonctions normales sont déjà prêtes ici.