Enigme: La bouteille empoisonnée
Vous êtes roi, et préparez votre mariage qui a lieu demain. Vous disposez d'autant de serviteurs que vous le désirez, et possédez 1000 bouteilles de vin pour le festin. On vous apprend qu'une des bouteilles parmis les 1000 est empoisonnée, et provoque la mort en moins de 24h, et ce quelle que soit la quantité absorbée. Quel est le nombre minimal de serviteurs que vous devez mobiliser afin de pouvoir isoler de manière certaine la bouteille empoisonée ? (on ne cherche pas à minimiser le nombre de morts mais bien le nombre de serviteurs mobilisés)
La première approche qui semble évidente est de prendre un serviteur pour chaque bouteille, et ainsi de voir qui meurt, pour trouver le poison. Ceci nous ferait 1000 serviteurs utilisés, on peut mieux faire.
Sans contrainte de temps, on aurait pu ensuite penser à une dichotomie : puisque le vin empoisonné est mortel même à petite dose, on pourrait faire des mélanges de vin. On sépare nos 1000 bouteilles en deux groupes, ce qui nous fait deux mélanges, qu'on fait gouter à deux serviteurs. On recoupe ensuite en deux le groupe du serviteur mort, etc, jusqu'à isoler le poison. A chaque étape on réutilise le serviteur qui n'est pas mort à l'étape précédente (ça fait vraiment tyran, mais c'est l'énonce qui est comme ça, je délègue toute responsabilité à l'auteur original). Ainsi, le nombre de serviteurs mobilisés serait égal au nombre de divisions de l'espace qu'on a du faire. Notons k ce nombre. On a du couper k-fois notre espace en deux afin d'arriver à 1. \(\frac{1000}{2k}=1\) \(2^k = 1000\) \(e^{kln(2)}=1000\) \[k=\frac{ln(1000)}{ln(2)}\]
On arrondit k à l'entier supérieur (on doit faire toutes les divisions de l'espace nécessaires, pas moins), ce qui nous fait 10.
Mais cette approche ne fonctionne que sans contrainte de temps, donc n'est pas viable ici.
On pourrait ensuite penser différement en se disant que un esclave peut gouter plusieurs bouteilles (ce qui est équivalent à la technique du mélange). Imaginons que nous repartitions les bouteilles dans une salle de sorte à ce qu'elles forment un carré (plus une rangée non complète car on ne peut pas faire un carré avec 1000 bouteilles). On associe à chaque rangée (colonnes et lignes) un serviteur. Celui-ci boit toute sa rangée. Ainsi, l'intersection des rangées des deux serviteurs morts nous donne la bouteille empoisonée. Ici on trouve sqrt(1000) = 31,6..., on fait prend donc un rectangle de 31*32 = 992, et on rajoute une rangée incomplète de 8, ce qui nous fait 64 serviteurs utilisés. C'est pas mal. Mais on peut encore faire mieux.
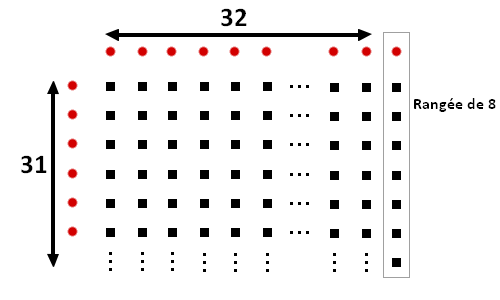
Les points rouges sont des serviteurs, les carrés noirs des bouteilles
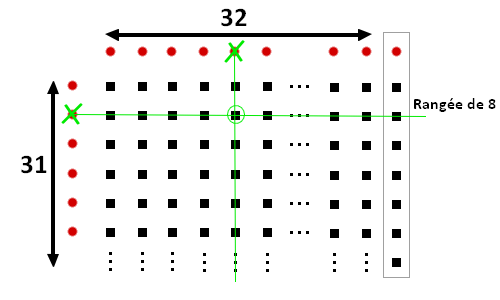 Le vert représente le poison. On trouve la bouteille empoisonée.
Le vert représente le poison. On trouve la bouteille empoisonée.
En fait le fait qu'un serviteur meurt ou non nous donne de l'information. Ce qu'on doit trouver, c'est comment cette information peut nous permettre d'identifier la bouteille empoisonée. Qu'à cela ne tienne, nous allons identifier chaque bouteille par un nombre binaire unique, et chaque serviteur par un numero (non binaire celui-ci).
Ce nombre binaire comportera autant de bits que de serviteurs, et la position d'un bit dans le mot correspondra à un numéro de serviteur. Si ce bit est à 1, alors cela signifie que ce serviteur aura bu dans cette bouteille.
Par exemple la bouteille 3 sera codée 0110 (si on code sur 4 bits, c'est à dire 4 serviteurs), ce qui signifie que les serviteurs 2 et 3 auront bu dedans.
Une fois que tout le monde a bu, on regarde les numéros des décédés : tous on leur bit à 1 dans la bouteille empoisonée, leur mort nous apporte l'information nécessaire.
Si par exemple on avait le serviteur 1 et le 3 de mort, alors la bouteille correspondante serait (0101), c'est à dire la numéro 5 !
Combien de serviteurs cette technique demande-t-elle? Il en faut assez pour encoder de manière unique chaque bouteille, donc il faut : , ce qui nous donne k = 10 serviteurs (même démo que précédemment).
Commentaires