SAX: Piecewise Aggregate Approximation
Problem: We have a series of n numbers that we want to divide into w slots. We want to compute the mean of each slot, how do we proceed when n is not divisible by w ? This is called a Piecewise Aggregate Approximation (PAA).
This question appeared when I read the SAX algorithm. It is used to convert a time series to a sequence of symbols. The trick is briefly explained in the paper, but the implementation requires a bit of thinking. Following schema is taken from the original paper, Experiencing SAX: a Novel Symbolic Representation of Time Series
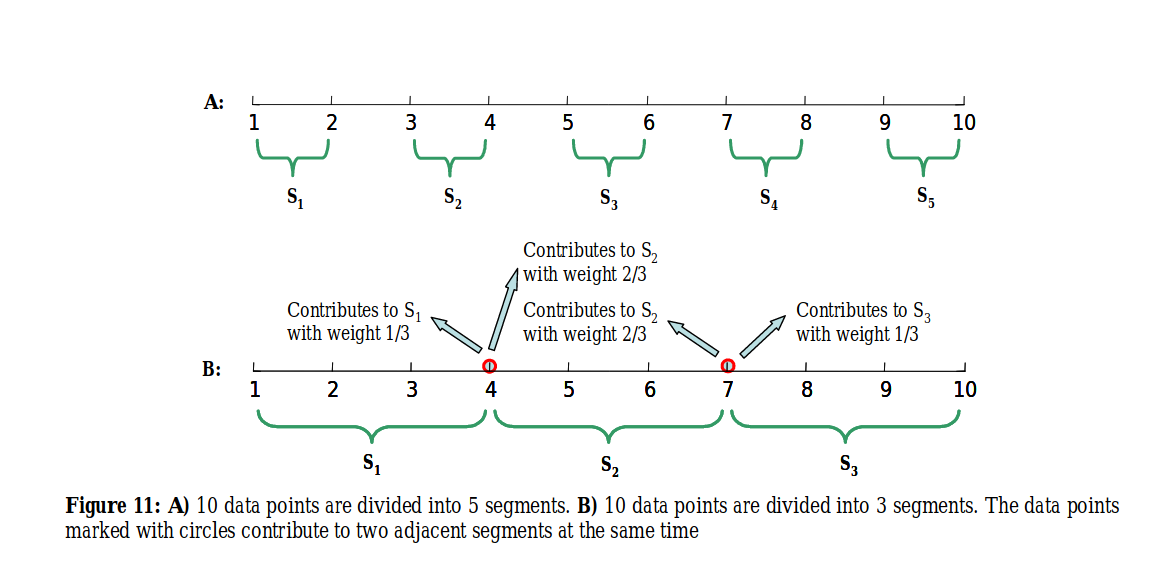
The natural way would be to consider each slot to be the size of the following equation (n//w is the floor division) \(\frac{n}{w} = n // w + \frac{n \% w}{w}\).
We start from index 0, we add n//w points, then we add a proportion of the next point, corresponding to (n%w)/w. For the second slot, we take the rest of the proportion of the previous point, we add n//w point, then the rest of the proportion of the last point so that the size of the slot is n/w. We keep doing this process until we reach the end of the series.
The issue with this strategy is that is quite difficult and inelegant to code.
There is a more elegant way. If we multiply n by w, we can consider that we repeat each point w times. What is the point of doing this ? We saw that the proportion of point we need to add to the current slot is a quantity that we will divide by w (it is (n%w)/w). Considering we repeat each point w times, we will be able to deal with a number of points that is an integer.
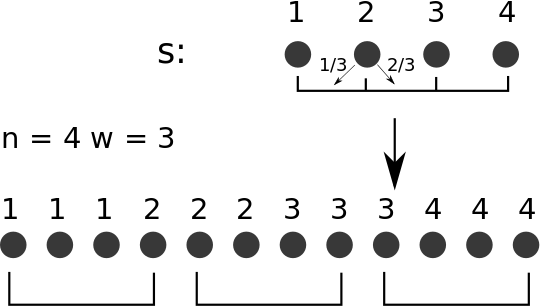
Now the slot does not have a size of n/w, but n. We sum each element of the slot, then we divide by n at the end: we will indeed get the mean of the slot. For example, the second slot in the picture above has a mean of (s[i] corresponds to the ith element of the serie):
\[\frac{\frac{2}{3}s[2] +\frac{2}{3}s[3]}{\frac{4}{3}}\]
Considering the new representation, the mean is:
\[\frac{2s[2] +2s[3]}{4}\]
which is the same.
Now the code:
def paa(s, w):
res = [0] * w
n = len(s)
for i in range(w * n):
idx = i // n
pos = i // w
res[idx] += s[pos]
res = [x / n for x in res]
return res
print(paa([1, 2, 0, 4, 3, 5, 6, -2, 3 -4], 4))
# >>> [1.3333333333333333, 2.4444444444444446, 4.888888888888889, -0.6666666666666666]
The following plot shows what the PAA looks like:
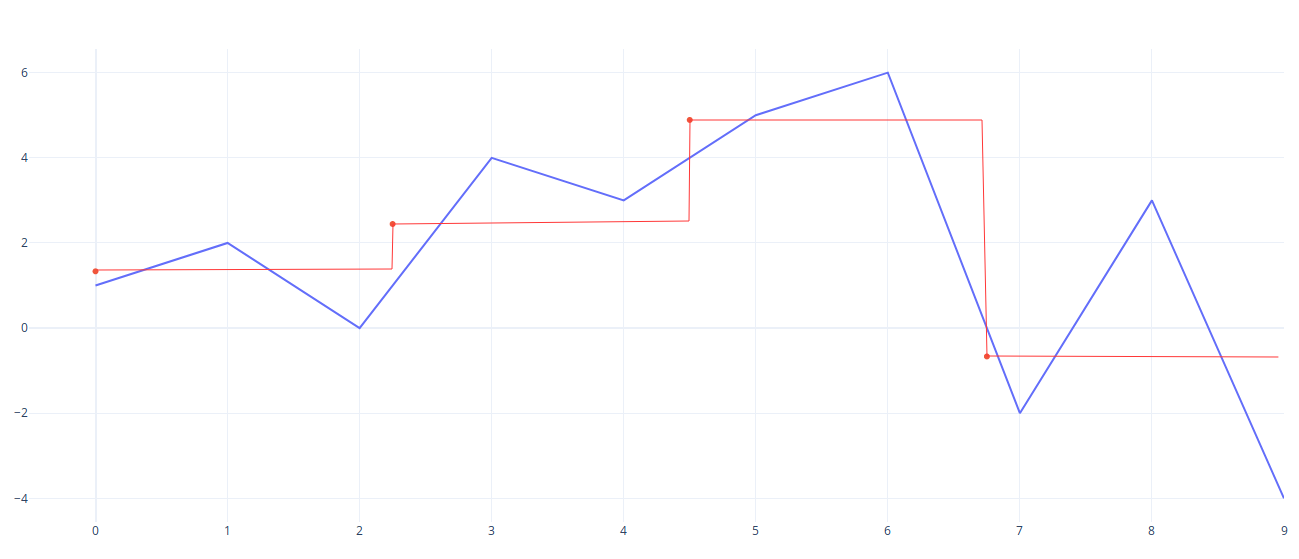
NB: Note however that this method has the disadvantage of increasing a lot the number of iterations. If you consider a long timeseries, it may be too long. If it is the case, you can choose to simply consider slot to have size n // w. If w is not divisble by w, we will have w + 1 slot, the last one having less points (you need to be aware of that).
Commentaires