Les problemes P, NP
En informatique, et en ingenierie en général, on peut voir notre métier comme une resolution successive de problèmes. Créer un site web, mettre en place une architecture big data, résoudre des bugs d'affichage sur une IHM, autant de problèmes que nous devons résoudre chaque jour.
Alors bien sûr, nous ne sommes pas capables de résoudre tous les problèmes, et on est même assez spécialisé : un ingenieur réseau ne va pas, a priori, savoir calculer les contraintes mécaniques auquel est soumis un avion de ligne afin d'optimiser son poids. Il y a des catégories de problèmes.
Concernant l'informatique, c'est pareil. Il y a des catégories de problèmes, et celles qui m'interessent dans ce billet sont celles qu'on nomme P, NP, NP-Complet, NP-difficile.
Pourquoi classifier les problèmes ?
Pour savoir si on est capable de les résoudre ! On se rend bien compte qu'entre trouver, par exemple, le maximum d'un tableau, et le problème de la somme de sous-ensembles, il y a une différence.
Savoir qu'on est tombé sur un problème NP-complet, par exemple, nous permet de savoir qu'on ne pourra pas le résoudre sur des cas trop compliqués, des générations de chercheurs s'y sont cassés les dents. Inutile donc de perdre trop de temps, avoir cette information peut permettre de mieux s'adapter à la situation, en proposant, par exemple, un algorithme qui s'approche de la bonne solution sans qu'on soit sûr qu'elle soit juste.
Prérequis (informel)
Complexité
Il faut savoir ce que c'est que la complexité d'un algorithme. L'explication mathématiques est un peu pompeuse, allez la chercher si vous voulez. En très gros:
La complexité d'un algorithme c'est à quel point l'algorithme prend du temps, en fonction de la taille de son entrée.
Par exemple trouver le maximum d'un tableau de taille n, on dit que sa complexité est de O(n) car pour le résoudre, on regarde n cases du tableau. Si on avait du parcourir deux fois le tableau, vous me direz qu'on noterait cela O(2n). Ca n'est pas faux, mais quand on varie seulement d'un facteur multiplicatif constant, on garde la notation O(n).
Maintenant, si on veut faire le produit cartésien du tableau avec lui-même, il faut itérer sur le tableau, et pour chaque itération réitérer sur tout le tableau pour trouver toutes les combinaisons possibles. On aura deux boucles imbriquées qui itèrent sur n, donc une complexité de O(n^2). Ca veut donc dire que le temps que va prendre mon algo dépend du carré de n, ce qui est moins bien que simplement de n.
Bon, je ne sais pas si j'ai été très clair, c'est une notion assez difficile à faire comprendre. Retenez que plus on a une complexité "simple", plus on est performant. Voici par exemple quelques complexités, classées par ordre croissant:
- O(1) (temps constant, super)
- O(n)
- O(n^2)
- O(2^n) (dur)
- O(n!) (RIP)
Les complexités de la forme O(n^p), avec p constant, sont des complexités dites polynomiales.
Les problèmes de décision
La plupart des classes suivantes portent sur des problèmes de décision: ceux-ci sont des problèmes qui attendent une réponse oui ou non, tout simplement.
Instance d'un problème
Une instance d'un problème est un problème dont on fixe les paramètres. Par exemple:
Problème: Trouver la moyenne de n valeurs.
Exemple d'instance du problème: n=3, et les valeurs sont 5, 6 et 2.
On a donc potentiellement une infinité d'instances pour un problème donné.
Les problèmes de classe P
Les problèmes de décision pouvant être résolus en temps polynomial font parti de la classe P.
Par exemple:
Etant donné n valeurs, la différence entre la valeur max et la valeur min est-elle supérieure à la moyenne ?
L'algorithme suivant a une complexité O(n) (donc polynomiale) et répond au problème: "calculer la moyenne des valeurs, trouver la valeur max, trouver la valeur min, les soustraire, comparer la moyenne et cette différence". Ce problème fait donc parti de la classe P.
Les problèmes de la classe NP
Les problèmes de décision dont les instances pour lesquelles la réponse est "oui" sont vérifiables en temps polynomial à partir d'un certificat (=une proposition de solution).
Par exemple le problème du voyageur de commerce (version décision):
Etant donné un ensemble de villes E, reliées entre elles par des chemins V, existe-t-il un chemin C passant par toutes les villes une seule fois et revenant à son point de départ, possédant une longueur inférieur à k ?
Pour ce problème, si on fournit une instance (E, V, k), càd un ensemble de villes, de chemins, et une distance, ainsi qu'un certificat, càd une proposition de solution (un ordre de chemins par lesquelles le voyageur de commerce doit passer), on peut verifier si cette solution permet de répondre oui ou non. En effet, il suffit de verifier si l'ensemble des chemins passent par toutes les villes une seule fois, et si la somme des longueur des chemins est inférieur à k.
En résumé, pour savoir si un problème est NP: on choisit une instance du problème, on fournit une hypothétique solution, on vérifie en temps polynomial si cette solution est vraie. Si c'est le cas, c'est NP.
Les problèmes NP-Complets
Les problèmes NP-Complets sont des problèmes NP, mais il existe une condition sumplémentaire pour être NP-Complet:
Un problème X est NP-Complet si tout autre problème NP-Complet Y peut-être réduit à X en temps polynomial.
Les chercheurs ont déjà effectué par mal de travail de ce côté là, on connait un certain nombre de problèmes NP-Complet, donc prouver que n'importe quel problème NP-Complet est reductible en temps polynomial à notre problème X suffit à prouver qu'il est NP-Complet.
Intuitivement, les problèmes NP-Complet sont des problèmes NP qui sont difficiles à résoudre : si les instances sont trop grandes, on ne sais pas résoudre le problème sans que cela prenne un temps considérable (et par considérable ça peut être un jour, un mois, un siècle selon la taille). Si on tombe sur un problème NP-Complet, il faut savoir qu'on est tombé sur un os, et qu'il est probablement vain de vouloir trouver un bon algorithme pour le résoudre.
Le problème du voyageur de commerce est NP-Complet, par exemple. En effet, le nombre de solutions possibles est exponentiel : si le graphe est complet (chaque ville est reliée à toutes les autres villes) avec n villes, on a un espace de n! possibilités !
(Détail) On a n possibilités pour le choix de la première ville, puis n-1 choix pour la seconde (on ne passe qu'une fois par ville), puis n-2 pour la troisième, etc, jusqu'à ce qu'on soit passé par les n villes, ce qui nous fait bien n! possibilités.
Les problèmes NP-Difficiles
Les problèmes NP-Difficiles sont des problèmes au moins aussi difficiles que les problèmes NP-Complets. De plus, ils ne sont pas forcément NP, ils ne sont donc pas forcément des problèmes de décision ! La formulation est surprenante, mais c'est ainsi.
Les problèmes NP-Complets sont inclus dans les problèmes NP-Difficiles. Par exemple, le problème de la somme des sous-ensembles : "Etant donné un ensemble E de n entiers, existe-t-il un sous-ensemble de E tel que la somme des éléments vaille 0 ?" Ceci est-un problème de décision qui est à la fois NP-Difficile et NP-Complet.
Le problème du voyageur de commerce dans son énonciation classique (et non pas décisionelle comme vu précédemment) est NP-Difficile, mais pas NP-Complet car ce n'est pas un problème de décision: "Etant donné n points (des « villes ») et les distances séparant chaque point, trouver un chemin de longueur totale minimale qui passe exactement une fois par chaque point et revienne au point de départ" (Wikipédia)
P != NP ?
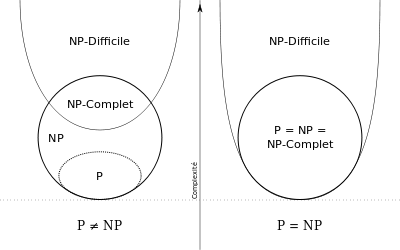
A l'heure actuelle, on a pas réussi à prouver mathématiquement que P = NP ou que P != NP. Il est très probable que la deuxième solution soit la bonne, car sinon cela signifierait qu'on pourrait trouver des réponses en temps polynomial à tous les problèmes NP, ce qui inclut les problèmes NP-Complet. Or ces problèmes Np-Complets sont bien connus depuis des années, moult gens brillants ont travaillé dessus et personne n'a trouvé d'algorithme qui résolve ce genre de problème en temps polynomial. D'ailleur celui qui prouvera que P != NP (ou que P = NP) se vera offrir la coquette somme d'un million de dollars.
Pour finir un petit schéma de Wikipédia, qui résume tout:
Commentaires