Résumé de statistiques/probabilités
Je suis en train de faire les cours du MIT sur les probabilités/statistiques (ici). Le titre officiel est "Introduction aux probabilités et statistiques", mais le cours est tout de même assez complet je trouve, donc je fais un résumé ici (ce n'est pas un vrai cours suffisamment, donc si vous ne connaissez pas un minimum, ça risque d'être un peu dur).
Loi de multiplication
S'il y a n façons de réaliser l'action 1, et m façons de réaliser l'action 2, alors il y a n*m façons de réaliser l'action 1 suivi de l'action 2.
Exemple: Combien y a-t-il de façons de tirer une paire d'as si l'on tire deux cartes d'un jeu de 52 cartes ?
Réponse: Il y a 4 as dans le jeu, donc 4 possibilités pour le premier tirage. Une fois qu'un premier as a été tiré, il n'en reste plus que 3 pour le second tirage, on a 3 possibilités. On a donc 4*3=12 tirages possibles. D'après la loi qu'on va voir juste après, on a donc une probabilité de:
\[\frac{12}{52*51} = \frac{1}{221}\]
Avoir une paire d'as avant le flop au poker est donc rare, puisqu'on a seulement 0.45% de chances.
Dénombrement
Dans le cas discret (par exemple tirer au hasard des cartes parmi un jeu de 52 cartes), si il y a équiprobabilité des issues, on fait souvent:
\[\frac{nombreIssuesQuiNousInteressent}{nombreIssuesPossibles}\]
Par exemple, trouver la probabilité de tirer un carreau (on parle de poker):
\[\frac{13}{52} = \frac{1}{4}\]
Arrangement sans répétition
Un arrangement sans répétition est noté:
\[A_n^{k}\]
Un arrangement avec répétions c'est prendre k billes parmi n dans un sac de billes, en tenant compte de l'ordre dans lequel on sort chacune d'elles. L'ensemble des issues (qui sont de longueur k) correspond aux arrangements sans répétition.
Par exemple j'ai un sac avec une boule verte (V), une bleue (B) et une rouge(R) (n=3), dans lequel je prend deux billes (k=2) l'ensemble des issues possibles est:
\({VB, VR, BV, BR, RV, RB}\)
Ce sont des tuples, l'ordre des éléments est importants.
Le nombre d'issues possibles est:
\[\frac{n!}{(n-k)!}\]
Pour notre exemple, cela correspond à:
\[\frac{3}{(3-2)!} = 6\]
En effet, pour prendre la première bille j'ai n possibilités, pour la deuxième, n-1, etc. Si on prend toutes les billes (k=n), on se retrouve avec n! possibilités, mais sinon, il faut diviser par (k-1)! pour éliminer les possibilités des billes restantes dans le sac après en avoir tiré k.
Arrangement avec répétition
Un arrangement avec répétition c'est tirer successivement k billes parmi n, en remettant chacune des billes tirées dans le sac au fil des tirages, et en tenant compte de l'ordre dans lequel les billes sortent.
Pour le sac exemple, les issues possibles sont:
\[{VV, VB, VR, BB, BV, BR, RR, RB, RV}\]
Le nombre d'issues possibles est:
\[n^k\]
Pour notre exemple, cela fait:
\[3^2 = 9\]
Nombre de permutations
Une permutation est une suite ordonné de n éléments. Pour un arrangement $BRVV$, une permuation possible est $RVBV$.
Une permutation correspond à un arrangement avec k=n Si les billes sont toutes disctinctes, on a $n!$ permutations possibles.
Dans le cas où les il y a plusieurs billes du même type, notons $nB$ le nombre de billes bleues, $nR$ et $nV$ le nombre de billes rouges et vertes. Notons que $nR + nV + nB = n$. On a alors un nombre de permutations possibles de:
\[ \frac{n!}{n_A!n_B!n_C!}\]
On divise par le produit des factoriels des nombre de billes de chaque type pour éliminer les permutations redondantes (avec la formule $n!$ on répète plusieurs fois la combinaison $BRVV$ par exemple, puisque les deux billes V peuvent échanger de place et donner le même résultat).
Combinaison sans répétition
Une combinaison sans répétition est notée:
\(C_n^{k}\)
Une combinaison sans répétition correspond au fait de tirer k billes parmi n, d'un seul coup. C'est un arrangement sans répétition dont on ignore l'ordre.
Pour le sac exemple, ça nous donne:
\[\{VR, RB, BV\}\]
Le nombre d'issues possibles est:
\[\frac{n!}{k!(n-k)!} = \frac{A_n^{k}}{k!}\]
Ici on trouve: \(\frac{3!}{2!(3-1)!} = 3\)
NB: Ceci est dû au fait qu'il y a une "correspondance" entre combinaison avec répétition et arrangement sans répétition. En effet, l'ensemble des arrangements qu'on peut générer à partir d'une combinaison (sans répétition) vaut k! : k possibilités de choix pour le premier élément, k-1 pour le deuxième etc.
Ce sont des ensembles, il n'y a pas d'ordre des éléments.
Combinaison avec répétition
Une combinaison avec répétition est une combinaison dans laquelle les éléments peuvent apparaître plusieurs fois. Par exemple faire 2 tirage de boules avec remise, si on s'intéresse uniquement aux résultats et pas à l'ordre dans lequel elles apparaissent, est une combinaison avec répétition.
Pour le sac exemple, ça nous donne: \(\{VR, RB, BV, VV, RR, BB\}\)
Le nombre d'issues possibles est:
\[\frac{(n+k-1)!}{k!(n-1)!}\]
Ca correpond à une combinaison sans remise de k éléments parmi n + k - 1.
Ici on trouve: \(\frac{4!}{2!(3-1)!} = 6\)
NB: On pourrait se dire qu'il suffirait de diviser les arrangements avec répétitions par k! pour trouver les combinaisons avec répétitions, comme on avait fait dans le cas sans répétition. Ca ne fonctionne pas car il y a des cas où les combinaisons et les arrangements se confondent. Par exemple l'ensemble {RB} correspond bien à 2! tuples (BR et RB), mais l'ensemble {RR} ne génère qu'un seul tuple RR !
Principe d'inclusion-exclusion
\[|A\cup B| = |A|+|B|-|A\cap B|\]
Probabilité conditionelle et théorème de Bayes
Probabilité conditionnelle:
\(P(A|B) = \frac{P(A\cap B)}{P(B)}\) si P(B) != 0
Loi des probabilités totales
Si l'ensemble des issues possibles est divisée en 2 parties disjointes B et C, pour tout évènement A, on a:
\[P(A) = P(A\cap B) + P(A\cap C)\]
Indépendance d'évènements
Deux évènements sont indépendants ssi: \(P(A\cap B) = P(A)*P(B)\)
Théorème de Bayes
\[P(B|A) = \frac{P(A|B)*P(B)}{P(A)}\]
Base rate fallacy
On peut utiliser le théorème de Bayes pour l'oubli de la fréquence de base (Base rate fallacy).
Enoncé 0.5% de la population est malade. On a un test de détection de la maladie, qui a un taux de faux positifs (= gens détectés mais non malades) de 5% et un taux de faux négatifs (= gens non-détectés mais malades) de 10%. On teste quelqu'un, le test est positif, quelle est la probabilité qu'il soit vraiment malade ? Réponse: 8.3%
Ce résultat paraît très surprenant à première vue. On a un classifieur qui a des taux d'erreur de l'ordre de 5 à 10%, et pourtant quand il détecte qu'on est malade, il y a très peu de chances qu'on le soit vraiment ! En fait il est très important de discerner precision, FPR (False Positive Rate) et FNR (False Negative Rate) pour ne pas faire d'erreur.
(je mets les notations en anglais, la plupart des articles sont en anglais donc ça permet moins de confusion)
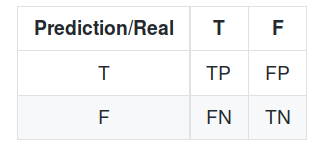
Verticalement on a la réalité, et horizontalement ce qui est prédit. En language courant, la traduction de ces sigles est la suivante:
- TP: Malades detectés comme étant malades
- FP: Non-malades detectés comme étant malades (erreur)
- FN: Malades non detectés (erreur)
- TN: Non-malades non detectés.
D'après l'énoncé et la définition du FPR (False Positive Rate), on a:
\(FPR = \frac{FP}{FP+TN}\)
C'est donc l'ensemble des non-malades détectés comme étant malades, divisé par l'ensemble des non-malades, càd la proportion d'erreur parmi les non-malades.
De même, le FNR (False Negative Rate):
\(FNR = \frac{FN}{FN+TP}\)
C'est donc l'ensemble des malades non-détectés, divisé par l'ensemble de malades, càd la proportion d'erreurs parmi les malades.
La précision, quand à elle, est définie comme suit:
\(Precision = \frac{TP}{TP+TN}\)
C'est l'ensemble des malades détectés sur l'ensemble des détections, càd la proportion de détections justes.
Ceci étant dit, revenons au problème. Si on me dit que le test est positif, cela signifie que je suis soit dans la catégorie des non-malades détectés (erreur), soit dans la catégorie des malades détectés. C'est là qu'il ne faut pas se tromper et dire que la répartition dans ces deux catégories est 5% et 95%, puisque c'est faux (contraire à la définition du dessus). Puisque la probabilité d'être malade est très faible (0.5%), le nombre de personnes détectées comme étant malades alors qu'elles ne le sont pas est très élevé (99.5% * 5% * n), en tous cas bien supérieur au nombre de personnes detectées comme étant malades et l'étant rééllement (0.5% * 90% * n). C'est pour cela qu'on trouve finalement une probabilité d'être effectivement malade faible, bien que le test soit positif.
Démo
Notation:
M: malade
!M: non-malade
D: détecté
!D: non-détecté
On veut la probabilité d'être malade sachant qu'on est détecté, càd P(M|D). On sait aussi que:
\(p(M) = \frac{0.5}{100}\)
\(p(D|\neg M) = \frac{5}{100}\)
(définition du faux positif)
\(p(\neg D|M) = \frac{10}{100}\)
(définition du faux négatif)
\(p(\neg D|\neg M) = \frac{95}{100}\)
(complémentaire du faux positif)
\(p(D| M) = \frac{90}{100}\)
(complémentaire du faux négatif)
En appliquant le théorème de Bayes, on a: \(p(M|D) = \frac{p(D|M)*p(M)}{p(D)} \)
Or, d'après la loi des probabilités totales, on a:
\[p(D) = p(D\cap M) + p(D\cap \neg M)\]
\[p(D) = 0.90*0.005 + 0.995*0.05\]
Donc on trouve:
\[p(M|D) = \frac{p(D|M)*p(M)}{p(D)} \approx 0.083\]
Se souvenir:
\[P(A|B)+P(\neg A|B) = 1\]
Variable aléatoire
Discrète
La fonction de masse (probability mass function = pmf) décrit la probabilité d'obtenir chacune des issues. On la note p(x). La fonction de répartition (cumulative mass function = cmf) décrit la probabilité d'avoir p(X < x). On la note F(x). Elle est définie comme suit:
\[F(x) = \sum \limits_{i=1}^x p(x)\]
L'espérance est la moyenne des issues. Elle est notée E(x). On a:
\[ E(x) = \sum \limits_{i=1}^n p(xi) * xi \]
Propriétés de E(x):
\[E(aX+Y+b) = aE(X) + E(Y) + b\]
La variance est l'espérance des carrés des écarts à la moyenne (le carré est là pour ne pas avoir de nombres négatifs). Notée Var(X):
\[Var(X) = E((X - \mu)^2)\]
Propriétés de Var(X): Si X et Y sont indépendantes
\(Var(aX + Y + b) = a^2Var(X) + Var(Y)\)
\[Var(X) = E(X^2) - E(X)^2\]
L'écart-type est un indicateur de la dipersion des mesures. C'est la racine carrée de la variance: \(\sigma = \sqrt{Var(X)}\)
Continue
La densité de probabilité (probability density function = pdf) la loi de probabilité des issues. La "probabilité unitaire" est f(x)dx. On la note f(x).
La fonction de répartition (cumulative density function = cdf) décrit la probabilité d'avoir p(X < x). On la note F(x).
Elle est définie comme suit:
\[F(b) = \int_{-\infty}^{b} p(x)dx\]
Propriétés de F(x):
\(p(a \le X \le b) = F(b) - F(a) \)
\(F'(x) = f(x)\)
\[p(a \le X \le b) = \int_{a}^{b} f(x)dx\]
L'espérance est la moyenne des issues. Elle est notée E(x).
On a:
\[E(x) = \int_{a}^{b} xf(x)dx\]
Propriétés de E(x):
\[E(aX+Y+b) = aE(X) + E(Y) + b\]
La variance est l'écart à la moyenne (au carré pour ne pas avoir de nombres négatifs). Notée Var(X):
\[Var(X) = E((X - \mu)^2)\]
Propriétés de Var(X): Si X et Y sont indépendantes
\(Var(aX + Y + b) = a^2Var(X) + Var(Y)\)
\[Var(X) = E(X^2) - E(X)^2\]
L'écart-type est un indicateur de la dipersion des mesures. C'est la racine de la variance:
\[\sigma = \sqrt{Var(X)}\]
Théorème central limite et loi des grands nombres.
Loi des grands nombres
Si on a un ensemble de n variables indépendantes et identiquement distribuées (i.i.d), plus n augmente, plus la moyenne des X s'approche de E(X).
Théorème central limite
On a un ensemble de n variables i.i.d. Soit Sn la somme de ces éléments, et Xn la moyenne de ces évènements. Ces deux variables suivent approximativement des lois normales (si n est suffisamment grand):
\[Zn = \frac{Sn - n\mu}{\sigma \sqrt{n}} = \frac{\bar Xn - \mu}{\frac{\sigma}{\sqrt{n}}}\]
Zn est la loi normale centrée réduite N(0,1)
Si on a 100 lancés de pièces succesifs, on peut estimer la probabiblité d'avoir plus de 55 faces, par exemple.
Distributions jointes et indépendance
Si on a plusieurs variables, on a une loi de probabilité à plusieurs variables (joint probability mass function) qu'on note p(xi, yi) pour le cas discret, et f(xi,yi) pour le cas continu.
Voir ce pdf pour avoir des exemples.
La fonction de répartition à plusieurs variables est:
\[F(x,y) = p(X \leq x, Y \leq y) = \iint\limits_{[a,y][b,x]} f(u,v)dudv\]
Pour retrouver la loi de densité de probabilité, il faut dériver selon les deux variables.
\[f(x,y) = \frac{\partial^2F(x,y)}{\partial x\partial y}\]
Loi de probabilité marginale
Une loi de probabilité marginale permet d'avoir le "comportement" d'une seule variable.
Si y prend ses valeurs dans [c, d], on a :
\[ fX(x) = \int_{c}^{d} f(x,y)dy\]
(on somme les valeurs de y).
Fonction de répartition
Pour avoir la fonction de répartition marginale, si X et Y prennent leur valeur dans [a,b]x[c,d], on a:
\[FX(x) = F(x,d)\]
\[FY(y) = F(b,y)\]
Indépendance
X et Y sont indépendantes ssi:
\(F(X,Y) = FX(x)FY(y)\)
ou encore:
\[f(x,y) = fX(x)fY(y)\]
Covariance et corrélation
Covariance
La covariance est une mesure de la façon dont deux variables varient ensemble. Par exemple la taille et le poids des girafes ont des covariances positives car quand l'une est grande, l'autre a tendance à l'être aussi. Inversement, quand la covariance est négative, quand une des variables est grande, l'autre a tendance a être petite.
\[Cov(X,Y) = E((X- \mu X)(Y- \mu Y))\]
Propriétés de la covariance
\[Cov(aX+b, cY+ d) = acCov(X,Y)\]
\[Cov(X1+X2, Y) = Cov(X1,Y)+Cov(X2,Y)\]
\[Cov(X,X) = Var(X)\]
\[Cov(X,Y) = E(X,Y) - \mu X \mu Y\]
\[Var(X+Y) = Var(X) + Var(Y) + 2Cov(X, Y)\]
Si X et Y sont indépendants, alors Cov(X, Y) = 0.
Attention la réciproque n'est pas vraie!
Corrélation
Le coefficient de corrélation permet de créer une mesure sans unité, adaptée pour comparer entre deux paires de variables.
\[Cor(X,Y)=\frac{Cov(X,Y)}{\sigma X\sigma Y}\]
Commentaires