Erreurs et manipulations en temps d'épidémie
Le sujet polarise énormément, je vais donc essayer de m'en tenir au fond pour tenter d'y voir plus clair parmi plusieurs erreurs ou manipulations que j'ai pu voir ces derniers temps. En particulier, un article a récemment été publié sur le blog de mediapart (il n'engage donc pas la rédaction) (MAJ: il a été retiré et republié ici). Il a été rédigé par Laurent Mucchielli, directeur de recherche au CRNS en sociologie, qui s'exprime donc en dehors de son domaine de compétence. D'autres auteurs, visiblement issus du monde scientifique et de la recherche (en pharmacie, médecine, informatique), ont co-signé l'article. A première vue, on peut donc se dire qu'on va avoir à faire à un travail scientifique juste et rigoureux. Voyons plus en détails.
"Beaucoup de malades sont vaccinés"
Un premier argument de cet article, repris dans plusieurs médias, est que "la majorité des personnes hospitalisées pour des formes graves sont désormais des personnes vaccinées." Ce n'est pas une statistique intéressante. Si tout le monde est vacciné, la proportion de personnes hospitalisées qui sont vaccinées est de 100%, et ce même s'il n'y a qu'une seule personne concernée. Peut-on pour autant conclure que le vaccin n'est pas efficace ? Non ! C'est une erreur classique appelée "base rate fallacy" dont on a déjà parlé ici.
En langage commun, on peut traduire cette proportion par la question "quelle est la probabilité d’être vacciné sachant qu’on est hospitalisé ?", qui peut être écrite p(vacciné|hospitalisé). En vérité ce qui nous intéresse ce serait plutôt p(hospitalisé|vacciné), càd le risque d'être hospitalisé sachant qu'on est vacciné, et de le comparer à la probabilité d'être hospitalisé sachant qu'on est pas vacciné.
Nous allons appliquer la loi de bayes. Le risque a priori d'être hospitalisé à cause du covid peut être estimé à 6,8% si on suit les premières estimations en début d'épidémie, et de 8,5% si on divise le nombre total d'hospitalisations en France par le nombre total de cas détectés. Notons que la véritable valeur est probablement plus basse, puisqu'il y a des cas de covid asymptomatiques qui n'ont pas été détectés. Cependant, cette valeur p(hospitalisé) sera la même dans le calcul de p(hospitalisé|vacciné) et de p(hospitalisé|non vacciné), puisqu’on va faire un ratio pour comparer, elle se simplifie et n’impactera pas le résultat.
De plus, en toute rigueur, on devrait préciser dans les notations que les estimations se font sous l'hypothèse qu'on attrape la covid (on l'enlève par souci de simplification). Dans ce cas là, on doit estimer la probabilité d'être vacciné sous l'hypothèse d'avoir contracté la covid. On doit donc réappliquer une loi de bayes à l'intérieur de notre calcul. On a :
\[p(vacciné|covid) = \frac{p(vacciné)}{p(covid)}p(covid|vacciné)\]
Admettons que la covid soit suffisamment virulente pour qu'on considère que la probabilité qu'on finisse par l'attraper soit de 100%. La probabilité a priori d'être vacciné est de 60%. Enfin, d'après l'étude sur le vaccin Pfizer, la probabilité de contracter la covid sachant que l'on est vacciné est de 95%. Pour d'autres vaccins ce serait moins. Admettons que ce soit 70%, pour essayer de prendre en compte que les vaccins sont moins efficaces avec les nouveaux variants. On a alors une probabilité d'être vacciné, sachant qu'on a la covid, de 42%, je vous épargne les détails de calcul (dans la suite des calculs cela correspond à p(vacciné), par soucis de simplification).
Enfin, en france, p(non vacciné|hospitalisé) = 85% (source)
Calculons donc la probabilité d'ếtre hospitalisé sachant qu'on est vacciné, avec les données françaises.
\[ p(hospitalisé|vacciné) = \frac{p(hospitalisé)}{p(vacciné)}p(vacciné|hospitalisé) \]
\[ = \frac{0.085}{0.42}*0.15\]
\[ = 3.0\%\]
Si on applique le même raisonnement pour calculer la probabilité d'être hospitalisé sachant qu'on n'est pas vacciné, on obtient:
\[ p(hospitalisé|non vacciné) = \frac{p(hospitalisé)}{p(non vacciné)}p(non vacciné|hospitalisé) \]
\[ = \frac{0.085}{0.58}*0.85\]
\[ = 12.4\%\]
Attention, encore une fois, cette estimation est faite en considérant une probabilité de 8,5% d'être hospitalisé si on contracte la covid, cette probabilité est discutable, mais elle ne change pas le ratio suivant:
En france, actuellement, on a 4 fois plus (12.4 / 3.0) de risques d'être hospitalisé si on n'est pas vacciné, dans l'hypothèse où l'on contracte la covid.
Remarque importante: il y a en plus au moins un biais supplémentaire dans ces données: on a donné le vaccin prioritairement aux personnes les plus vulnérables. Ainsi, on compare une population vaccinée qui est plus fragile (âge, comorbidités) à une population non-vaccinée plus résistante, ce qui peut avoir tendance à faire baisser les "résultats" du vaccin.
C'est pour cette raison qu'on fait des études expérimentales, où on prend deux groupes de personnes suffisamment grands. L'aléatoire et la taille des groupes permet de faire en sorte qu'ils soient comparables pour d'autres variables qui viendraient influencer les résultats (par exemple l'âge, qui augmente la mortalité).
Ces études existent, puisqu'elles sont nécessaires pour pouvoir attester, de manière objective, de l'efficacité et de la sûreté d'un vaccin. Par exemple, dans la publication relative au vaccin Pfizer, on a fait deux groupes aléatoires de plus de 21 000 personnes, un groupe auquel on a donné le vaccin, un autre où on a donné un placebo. On a ensuite comparé les nombres de personnes ayant contracté la covid dans chaque groupe (7 pour le premier, 162 pour l'autre), ce qui nous permet d'estimer (avec un test statistique) que le vaccin protège à 95% du covid, à l'heure de l'étude.
Pourquoi alors semble-t-on dire que le vaccin n'empêche pas d'attraper la covid ? Plusieurs hypothèses sont possibles, comme le fait que le virus ait muté, qu'il y a ce biais de donner un vaccin à une population plus vulnérable, qui fait baisser son score, entre autres. Je ne me risquerais pas à en dire plus, ce n'est pas mon domaine de compétence. En tous cas, retenons que les données actuelles nous donnent l'estimation suivante: on a 4 fois plus de risques d'être hospitalisé à cause du covid en France actuellement si l'on n'est pas vacciné que si on l'est.
Confondre causalité et corrélation
L'article cite deux chercheurs, qui sont aussi co-signataires: Emanuelle Darles et Vincent Pavant. Dans cette vidéo, Mr Pavant utilise un modèle (qui peut paraître complexe au premier abord, et même inadéquat au second) et l'adapte à une courbe d'évolution de la mortalité, dont il ne prend que la moitié pour ensuite créer de nouvelles données qui l'arrangent, afin de tenter de montrer la pertinence de son modèle. Il conclut ainsi que "le lien entre vaccination et mortalité est certain". Ce raisonnement est faux. On ne peut pas prendre une courbe, placer la date de début de vaccination et dire "le nombre de mort augmente après le début de la vaccination, donc la vaccination tue des gens" (c'est finalement ce qu'il fait et ce que font les autres intervenants) En anglais ce phénomène s'appelle "spurious correlation", et il y a un site qui les répertorie.
Sans rentrer dans les formalisations mathématiques rigoureuses, on dit que deux variables sont corrélées quand elles varient de la même manière.
Par exemple, chez les êtres humains la taille est assez bien corrélée à la masse: plus l'on est grand, plus on a tendance à être lourd, et inversement. La causalité elle, consiste à dire qu'une variable cause/influence une autre. Par exemple, la quantité d'alcool que j'ingère cause une augmentation de mon taux d'alcool dans le sang. Les recherches de causalités peuvent être des problématiques très difficiles, sur lesquelles travaillent de nombreux chercheurs.
Par exemple ici, on peut voir que la consommation de mozzarella est corrélée au nombre de doctorats en génie civil décernés aux Etats-unis.
Est ce qu'il y a un lien entre ces deux variables ? Probablement pas. Mais à cause de l'aléatoire de notre monde, on peut trouver des corrélations, par "chance", sans qu'il y ait de causalité. De même, il peut y avoir corrélation entre deux variables sans que l'une soit la cause de l'autre, mais plutôt qu'il y ait un autre phénomène caché qui influence ces deux variables.
Par exemple, (repris du livre Prenez le temps d'y penser, B. Benamran), les gens qui se couchent avec leurs chaussures ont mal à la tête le lendemain. Est-ce que pour autant le fait de dormir avec ses chaussures cause le mal de tête ? Non ! Il y a une variable cachée qui est "les personnes qui boivent trop s'endorment avec leurs chaussures". Ainsi, cette variable cachée a causé l'endormissement avec les chaussures, et le mal de tête.
Revenons à notre épidémie. On constate qu'à partir du moment où on vaccine, la mortalité augmente. Est ce qu'on peut conclure que le vaccin cause la mort ? Non. Très probablement, ce qui se passe c'est que l'épidémie repart vite, donc on vaccine pour éviter des morts du covid.
Le vaccin permet d'éviter des morts, mais il y en a tout de même à cause de l'épidémie. Ici la variable cachée, qui cause la vaccination et l'augmentation du nombre de morts, c'est tout simplement l'épidémie. Notons qu'en toute rigueur, il faudrait valider cette hypothèse expérimentalement.
Ce qui tombe "bien" (si tant est que nous puissions parler ainsi étant donné la situation), c'est que nous avons déjà ces données, puisque certains pays ont beaucoup vacciné, quand d'autres non (source):
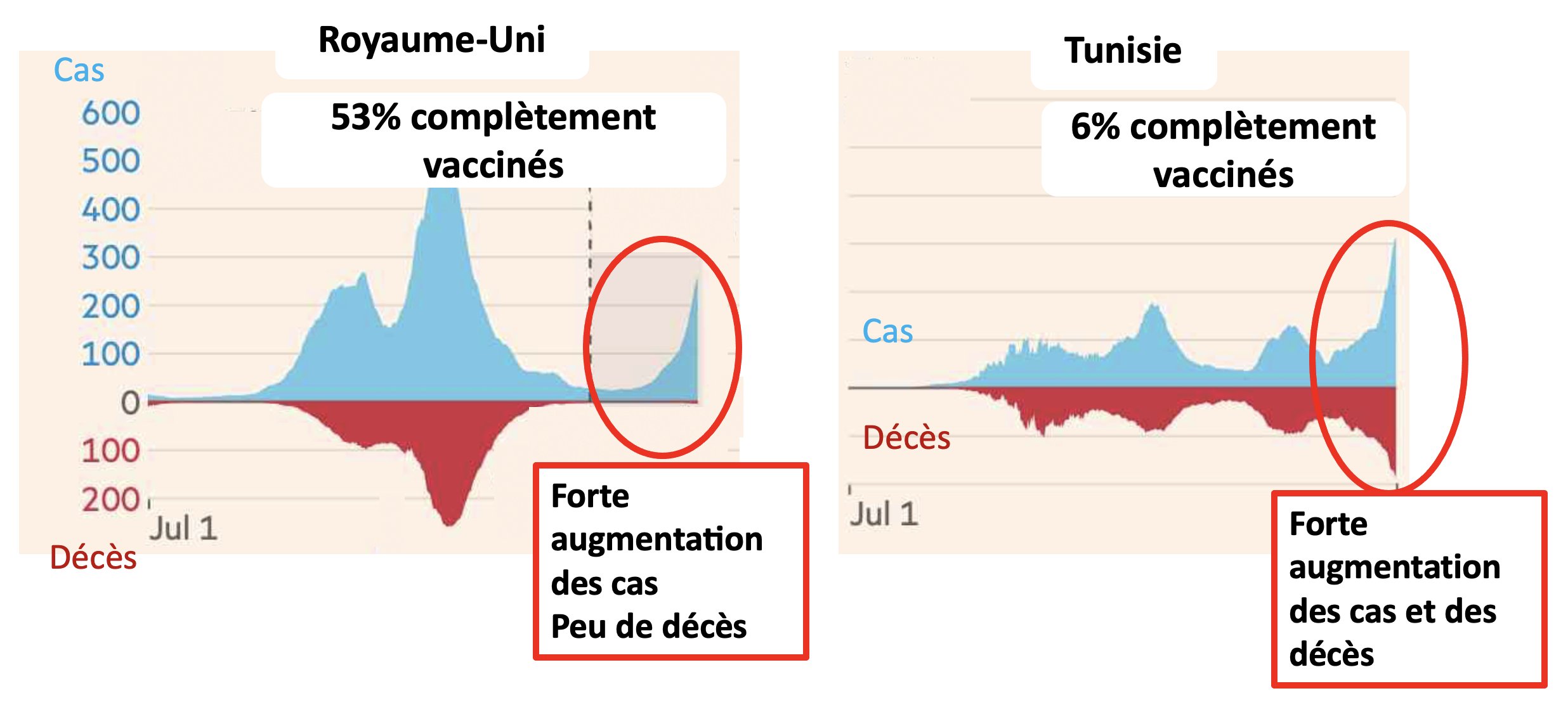
Ici on a bien deux groupes aléatoires, de grandes tailles, ce qui nous permet d'avoir une bonne idée de l'influence du vaccin sur la mortalité. Dans celui vacciné on a très peu de décès, dans celui non-vacciné, on en a beaucoup plus. Ceci n'est pas une preuve en soi, si on veut être rigoureux, car il faudrait que l'experience se passe dans le même pays, avec le même climat, etc., pour être sûr qu'il n'y ait pas de facteur confondant (biais), mais c'est tout de même très encourageant.
Autre remarques diverses
- Dans l'article de Mr Mucchielli, il est assuré que la balance bénéfice-risque pour les jeunes est très mauvaise. Si on se réfère à la source qui est citée, on se rend compte qu'on compare les risques de la covid chez les jeunes par rapport au risque du vaccin dans la population générale. On compare donc des choses qui sont différentes, les conclusions sont donc fausses. Dans les rapports qu'ils citent, on a par exemple qu'un seul cas grave pour les 0-15 ans, et on voit que la médiane des décès pour les vaccinés est de 76,2 ans...
- On fait l'hypothèse que les morts après le vaccin sont liés au vaccin dans cet article. Dans les rapports du CRPV sur le moderna, il est pourtant bien écrit "Aussi ce rapport mensuel présente uniquement les effets indésirables pour lesquels le rôle du vaccin est confirmé ou suspecté". Encore une fois, trouver la causalité est difficile. Dans les conclusions des rapports, il est clairement dit qu'il n'y a pas de certitude sur le fait que ce soit le vaccin qui cause les morts. Il faut être prudent sur ces affirmations. Si on donne une banane à manger à 100 000 personnes, il y aura probablement quelques dizaines de personnes qui auront des effets indésirables, et des morts. Doit-on en conclure que les bananes causent la mort ? Non ! Dans le cas présent, je ne suis pas compétent en pharmacologie pour pouvoir juger. Je m'en remet donc aux publications des experts qui concluent que non. Ce que je peux dire par contre, c'est que l'article au mieux se trompe, au pire manipule les données.
- L'article présente volontairement des pourcentages qui font peur. Par exemple pour pfizer, les données sont écrites en absolu, et on écrit subitement un pourcentage: 27.7%. Cette proportion reste en tête, si on lit un peu vite on se dit que les formes graves sont très courantes, alors qu'il s'agit seulement de la proportion d'effets graves parmi les indésirables. En fait, si on calcul le nombre de décès parmis toutes les injections sur pfizer, par exemple, on trouve 0.0018%.
- Si on compte tous les cas graves pour le vaccin, alors il convient de compter aussi tous les cas graves pour le covid (hospitalisation, covid long etc), sinon on ne compare pas la même chose. Ou alors on compare le nombre de morts, et dans ce cas les calculs sont beaucoup plus raisonnables.
- Aucune citation de toute la littérature scientifique qui ne va pas dans le sens du/des auteur(s). C'est assez perturbant quand on voit que l'article se dit de vouloir "observer froidement les données", et dénonce une "idéologie de la vaccination intégrale".
- Cet article n'est pas un article scientifique revu par les pairs. Les erreurs pointées ici (entre autres) n'auraient pas permis une telle publication dans un journal/une conférence serieux/sérieuse.
Conclusion
L'isolation de la causalité est un problème difficile, c'est une des raisons pour lesquelles des gens passent leur vie à faire de la recherche. Il y a plusieurs réflexes qu'il est bon d'avoir lorsqu'on nous présente des chiffres et conclusions toutes faites: qui parle ? Ces personnes s'expriment-elles dans leur domaine de compétence ? Avons-nous à faire à un article scientifique revu par les pairs ? Où a-t-il été publié ? A quoi correspond concrètement la proportion/la statistique qu'on nous présente ? Et surtout, il faut se méfier des corrélations, qui ne sont pas forcément des causalités. En particulier, quand on présente un graphique et qu'on en conclut "parce que ça se voit", il faut bien réfléchir à ce qu'il y a derrière. Est ce que c'est une étude expérimentale où on prend deux groupes aléatoires de grandes tailles pour vraiment étudier l'impact d'une seule variable, ou sont-ce des données observationnelles (càd observations sans avoir défini un plan d'expérience au préalable, où on ne contrôle pas le processus de génération de données), qui peuvent donc comporter des biais ? Pour une explication visuelle et bien vulgarisée, voir ici.
On a finalement aussi estimé ici qu'une personne moyenne de la population française, si elle attrape la covid actuellement, a quatre fois plus de risques d'être hospitalisée si elle n'est pas vaccinée. Enfin, les données comparatives entre l'angleterre et la tunisie semblent bien confirmer que la vaccination protège des risques de décès dus au covid.
NB: Merci à Anes Bendimerad, Aurélie Gabriel et Nicolas Nativel pour leurs relectures et critiques.
Commentaires